提到“克莱因”，大家第一反应应该是法国艺术家伊夫·克莱因，在上世纪60年代展示的一种混合颜色，在现代社会已经成为了高级和温柔的代表。

克莱因蓝

但是今天，我们要讲的不是这个“克莱因”，而是一个神奇的瓶子“克莱因瓶”。

而即便我们将其叫做“克莱因瓶”，它也不是一个真正意义上的瓶子，因为在它的底部有一个洞，我们根本无法将其填满。

接下来我们就来了解一下，神奇的“克莱因瓶”是什么？为什么将地球上的水倒进去，也装不满？

克莱因瓶

“克莱因瓶”无法真的存在于三维空间

最开始数学家菲利克斯·克莱因，在1882年提出它的时候，用的是德语“Kleinsche Fläche”，正确的翻译应该是“克莱因平面”。

只是后来人们在抄写的过程中，将“Fläche”，抄成了“Flasche”，于是就变成“克莱因瓶”了。

之所以要提到这个典故，是因为我们根据它的描述，制作出来的图像其实就和瓶子没什么两样。

菲利克斯·克莱因

在数学领域，克莱因瓶值得是一种无定向性的平面，就像在二维空间中一样，没有内外之分。

在拓扑学中，它指的就是一个不可定向的拓扑空间。

所以对其进行理解后，我们可以将克莱因瓶表述为：将一个底部有洞的瓶子，进行延长，使得瓶颈能够扭曲进入瓶子内部，最后于底部的洞连接起来。

如果是这样的话，那么一只蚂蚁在瓶子的内部爬行，就不需要爬到表面就可以来到瓶子外面了。

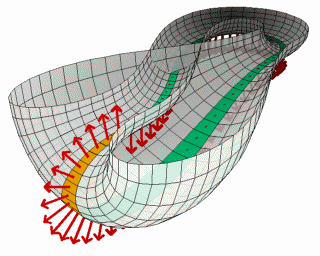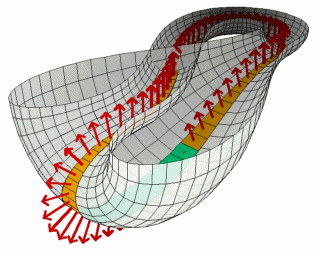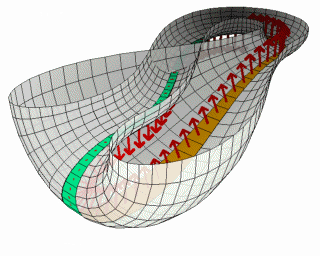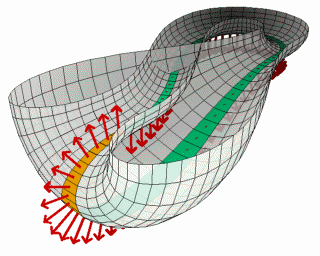
克莱因瓶

两个莫比乌斯环构成“克莱因瓶”

怎样可以形象地理解这样的结构呢？我们可以从莫比乌斯环来进行理解。

二维空间属于平面，这个大家都知道，也就是拥有正反两面的纸条。

如果在这个纸条上，存在一个二维生物，它此时需要从正面来到反面的话，必须要绕过纸条的边缘才能抵达，当然如果它有本事直接穿过纸条也可以。

但现在我们不想这个二维生物这么麻烦，于是将的一端翻转180°（180°的奇数倍都行），然后再将两端粘在一起，也就是”莫比乌斯环“。

莫比乌斯环

这个具有单侧曲面的二维环状结构，是1858年数学家奥古斯特·莫比乌斯发现的。

我们可以发现，如果将蚂蚁放在这样结构的纸条上，它既不需要经过边缘，也不需要穿过平面，就可以达到另一面了。

并且这样的结构，可以说是无限循环的，所以现在很多商家都将其视为爱情永恒的象征，制作出了类似结构的“莫比乌斯环”戒指。

莫比乌斯环戒指

这里的莫比乌斯环还存在着边缘，但如果我们将两个莫比乌斯环合在一起，那么它们的边缘就可以完全连接起来，于是就可以得到一个封闭的结构。

最后呈现出来的其实就是一个，没有内外之分，能够直接从内部进入外面的“克莱因瓶”。

关于莫比乌斯环属于几维空间，很多人多有争议，但是既然我们能够在三维空间看到并将其制造出来，那就可以将其视作三维空间的曲面。

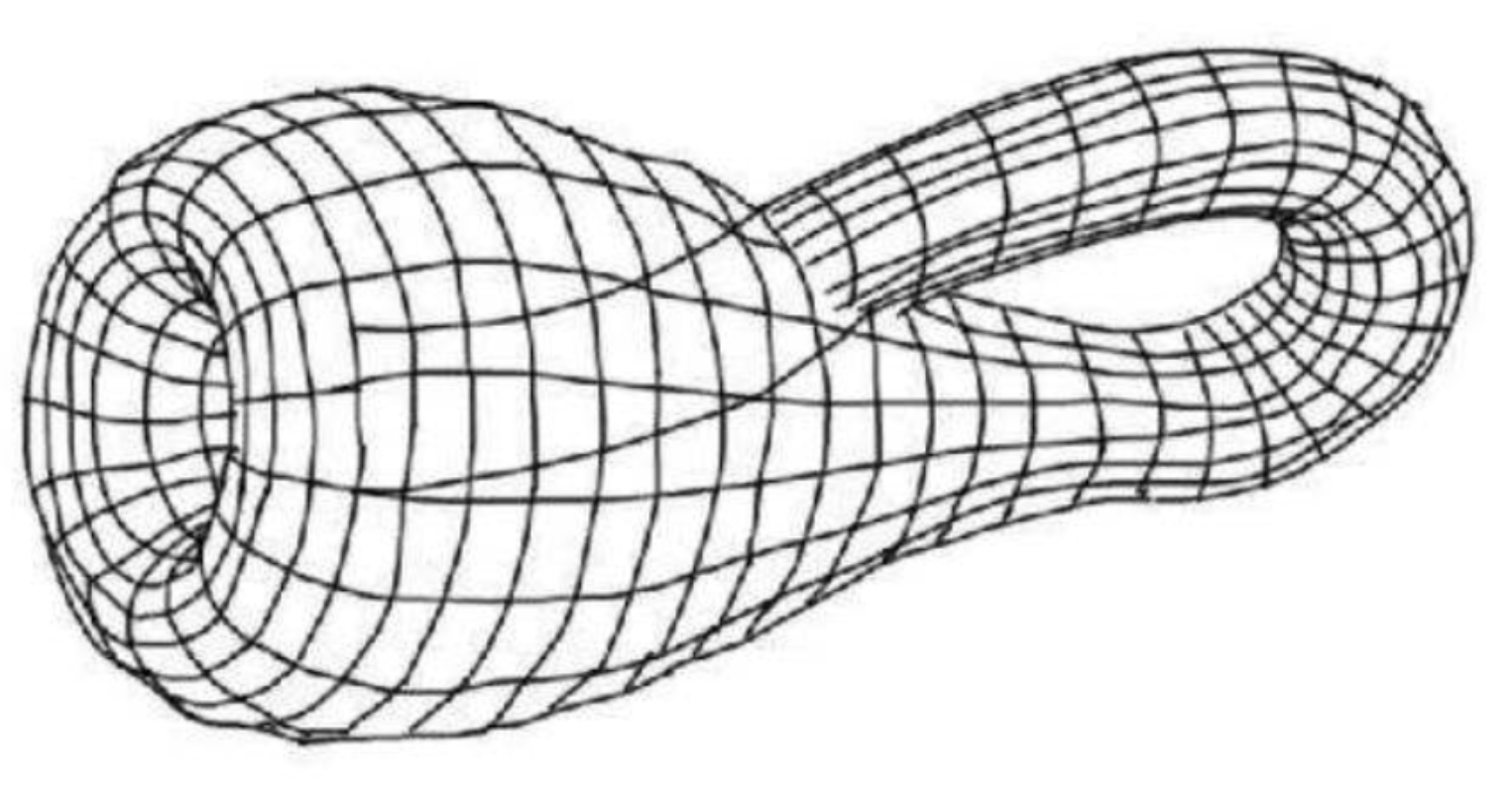
克莱因瓶

而这样两个莫比乌斯环的叠加，显然就上升了“克莱因瓶”的维度，使得其只能在四维空间以上的世界存在。

莫比乌斯环能够无限循环，那么两个加在一起，也可以实现这种永恒，所以我们才会说，如果这种瓶子真的存在，那么即便将地球上的水都倒进去，也没有办法将其装满。

因此很多在市面上售卖的克莱因瓶，其实都是假的，将水倒进去后，随随便便就能装满，这不过商家是为了寻一个赚钱的门道罢了。

不是真的克莱因瓶

四维空间是什么？

那么在四维空间中，世界又是怎样的呢？

我们常说的四维空间又称“欧几里得四维空间”，这其实是一个数学概念，所以一定要和爱因斯坦提出的“四维时空”区分开。

科学家们根据现代科学知识体系，甚至总结出了11个维度空间，也就是在数学和物理学中，我们可以将n个数的序列，理解成一个n维度空间中的位置。

四维空间

在我们所处的三维空间中，存在三对主要方向，上下对应的是高度，南北对应的是维度，东西对应的就是经度。

这三对方向在空间中属于两两正交，也就是两两成直角，在数学上对应的就是咱们的x，y，z坐标轴了。

所以处于三维空间的人，可以看到二维生物无法看到的被遮挡在墙背后的物体，并且能够在不破坏空间的前提下就能将其拿出来。

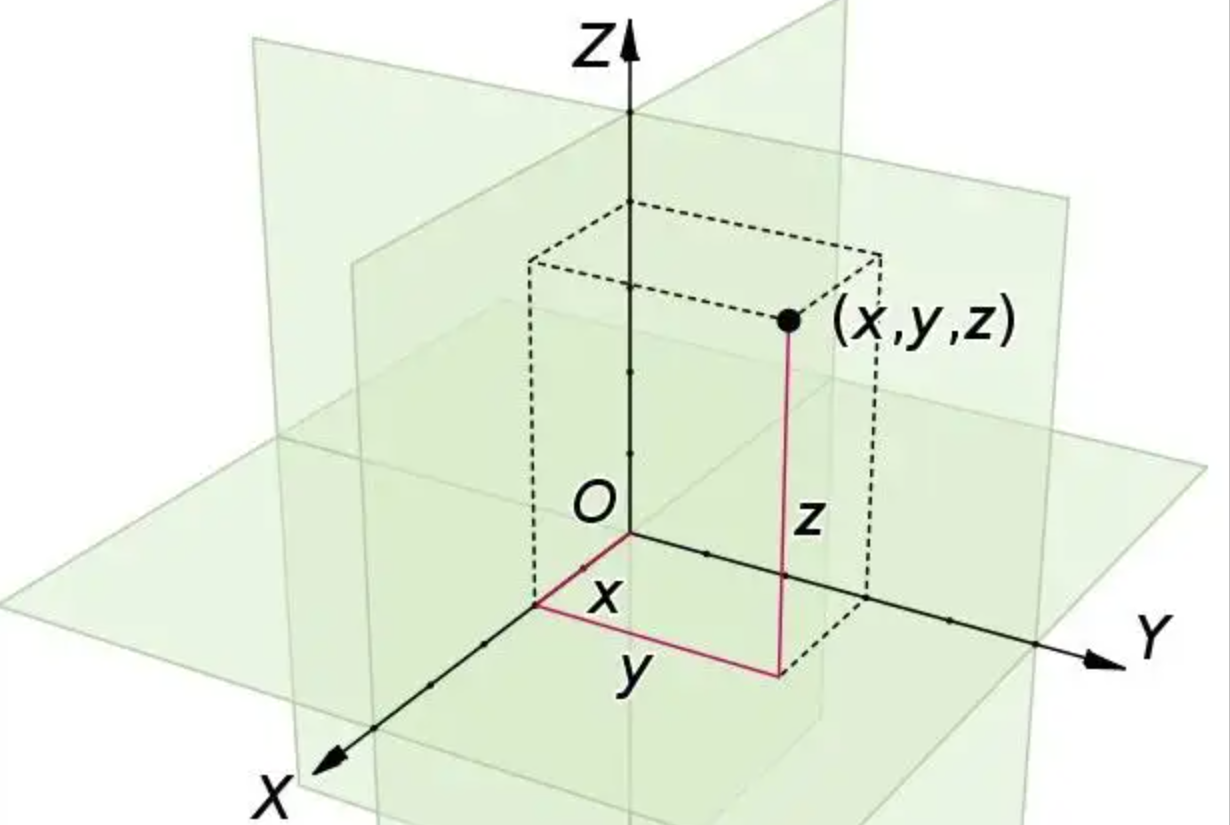
三维空间的坐标轴

而在四维空间，就多了一对可以和其他三个主要方向垂直的主要方向，对应的坐标轴为w轴。

这时候处于四维空间的生物，就可以看到三维生物无法看到的事物，并且轻松将其取出。

如果按照空间的组成来说，一维空间就是点，二维空间就是将多个点组合在一起，形成的平面，而三维空间就是多个平面组成的“曲面”。

三维空间

那么再这样推算下去，四维空间就是由多个三维空间组成的了。

然而由于人类现在作为三维生物，对于四维空间只能进行猜测，并基于现象总结，我们无法判断其正误，所以即便我们看到了一些现象，也无法确定这是四维空间引起的。

在三维空间中的“克莱因瓶”

市面上仍旧有很多模仿的“克莱因瓶”，虽然从表面上看起来，似乎不需要经过瓶子外部就可以从内部出来。

只是形状相似而已

但实际上，这样的瓶颈和瓶身是相交在一起的，这就和我们概念中的“克莱因瓶”有很大区别，因为它根本就是自己穿过了自己的表面。

所以在三维空间中，人类无法真的将两个莫比乌斯环的边缘完全连接起来，除非要穿过它的表面。

毕达哥拉斯杯与九龙杯

我们虽然在现实世界中无法将克莱因瓶制造出来，但是确实存在一种永远装不满的杯子，那就是西方的毕达哥拉斯与中国古代的九龙杯。

毕达哥拉斯和他的杯子

这两个杯子运用的原理其实运用的原理是相同的，我国的九龙杯，被称为公道杯，是明朝年间由工匠所制。

而毕达哥拉斯杯，也叫毕达哥拉斯贪婪坦塔罗斯杯，则由古希腊科学家毕达哥拉斯发明。

在杯子内部，有一条水位线，如果杯中的液体低于水位线时，它就和普通的杯子一样别无二致。

但是如果当杯子

里的水超过水位线时，杯中的液体就会通过虹吸现象从杯底漏出去。

利用虹吸现象的杯子

两个杯子告诉我们后人的，就是“知足者酒（久）存，贪心者酒（久）尽”，也就是说我们对待生活，知足常乐就好了。

虹吸效应

这其中应用到的虹吸效应，其实就是利用压强差的原理，在密闭的容器中，液体的高度相等，那么压强也就相当。

我们在家中就可以做这样的实验，将两个杯子叠放在一起，然后将上方的杯子打孔，与下方的杯盖贯通，将我们平时用的U型虹吸管放置在其中。

在家也能做的实验

随后往上方的杯子中加水，当水淹没吸管时，其中就空气流动了，于是两个杯子的压力就不一样了，在压强的作用下，虹吸管就会将水吸到下面的杯子中去。

所以在文献中，如果皇帝使用九龙杯，将美酒斟满的话，反而一口都喝不到，而如果只倒半杯，那就可以心满意足地喝到啦。